I am in love with this comment and want to have its babies:

pi appears as a constant in many formula of physics. General relativity says that it isn’t constant. Is it the origin of the pi particle, aka pion?

A curmudgeonly literalist might, when faced with a question such as this, harrumph a simple “No.” A more loquacious sort might explain that general relativity does not say that π is not a contstant. Pi is not a parameter of physics like the fine-structure constant, which could conceivably be different or even variable from place to place. It’s a universal answer to a fixed question, to wit: what is the ratio of the circumference of a circle to its diameter, as measured in Euclidean geometry? The answer is of course 3.141592653589793…, or any number of representations in terms of infinite series.

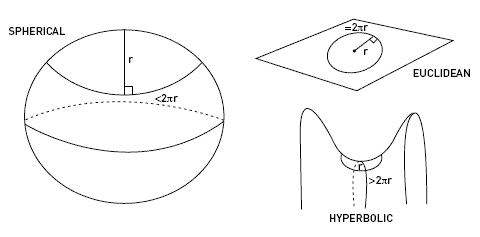
But the point of the question is that GR says we don’t live in Euclidean space; we move through a curved spacetime manifold. That’s okay. In a curved space, we could imagine defining the “diameter” of a circle as the maximum geodesic distance connecting two of its points, and taking the ratio of the circumference with that diameter, and indeed it would typically not give us 3.14159… But that doesn’t mean π is changing from place to place; it just means that the ratio of circumference to diameter (defined this way) in a curved space doesn’t equal π. If the circumference/diameter ratio is less than π, you are in a positively curved space, such as a sphere; if it is greater than π, you are in a negatively curved space, such as a saddle. Geometry can also be much more complicated than that, with different ratios depending on how the circle is oriented in space, which is why curvature is properly measured by tensors rather than by a simple number.

(Parenthetically, one of the dumbest mathematical arguments ever given was put forward by the world’s smartest person, Marilyn Vos Savant. The columnist wrote an entire book criticizing Andrew Wiles’s proof of Fermat’s Last Theorem. Her argument: Wyles made use of non-Euclidean geometry, but what if geometry is really Euclidean? Touche!)

However … despite the fact that π doesn’t really change from place to place in general relativity, the geometry does change from place to place, and there is a particle associated with those dynamics — the graviton. Although the formulation of the original question isn’t accurate, the spirit is very much in the right place. And I, for one, will henceforth be perpetually sad that the physics community missed a chance by attaching the word pion to the lightest quark-antiquark bound state, rather than to the particle associated with deviations from Euclidean geometry. That would have been awesome.